1. El peso del gasto autonómico

En los últimos días se ha hablado mucho de financiación autonómica. La necesidad de dar satisfacción a las demandas de ERC ha llevado a una propuesta de modificación de ese modelo de financiación que no es más que una ceremonia de la confusión orientada a disimular lo que en realidad supone: un traje a medida para los nacionalistas.

Ahora bien, creo que es conveniente evitar caer en la trampa de los detalles de la propuesta y abordar el coste del modelo autonómico desde otra perspectiva, una que, con frecuencia, se pretende eludir. Diría que para que no nos acabemos de dar cuenta de la estructural perversión del sistema.

A continuación, compartiré algunos datos e impresiones que pretenden que tengamos una idea más cabal de qué es lo que realmente se esconde tras estos debates. Para ello partiré del gasto autonómico; esto es, el dinero que gestionan las Comunidades Autónomas, comparado con el dinero que gestiona el Estado, el gasto de pensiones, el presupuesto de la administración local y el total del PIB español.

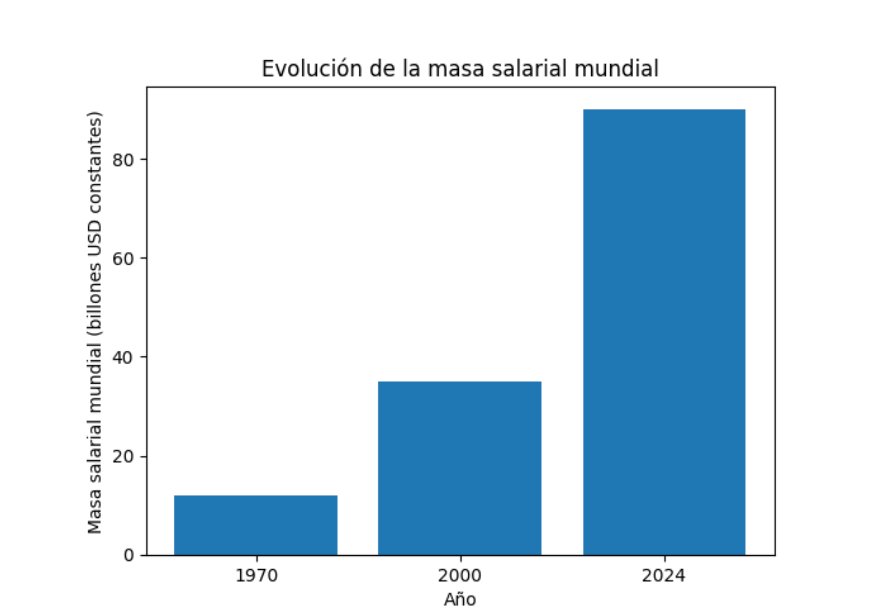
El conjunto del gasto autonómico es mayor que el gasto en pensiones y que el dinero que gestiona directamente el Estado. Por supuesto, es mucho mayor que el gasto de las administraciones locales. Tiene lógica, por otra parte, porque las Comunidades Autónomas tienen atribuidas las competencias de mayor peso económico: educación y sanidad. El gasto público en estos dos ámbitos es aproximadamente un 10% del PIB; ligeramente por debajo del gasto público en pensiones.

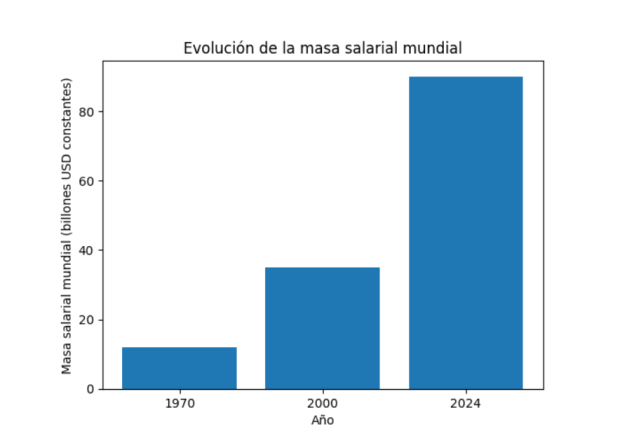
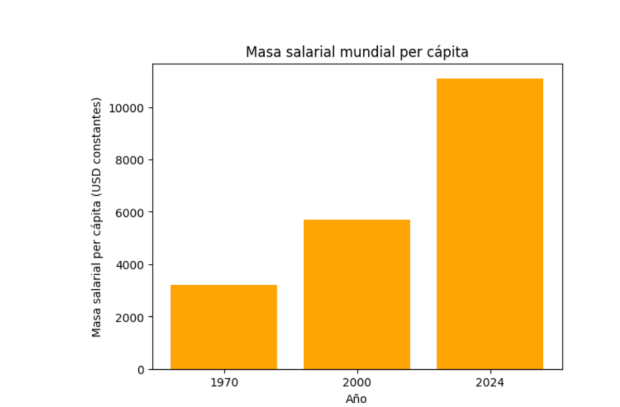
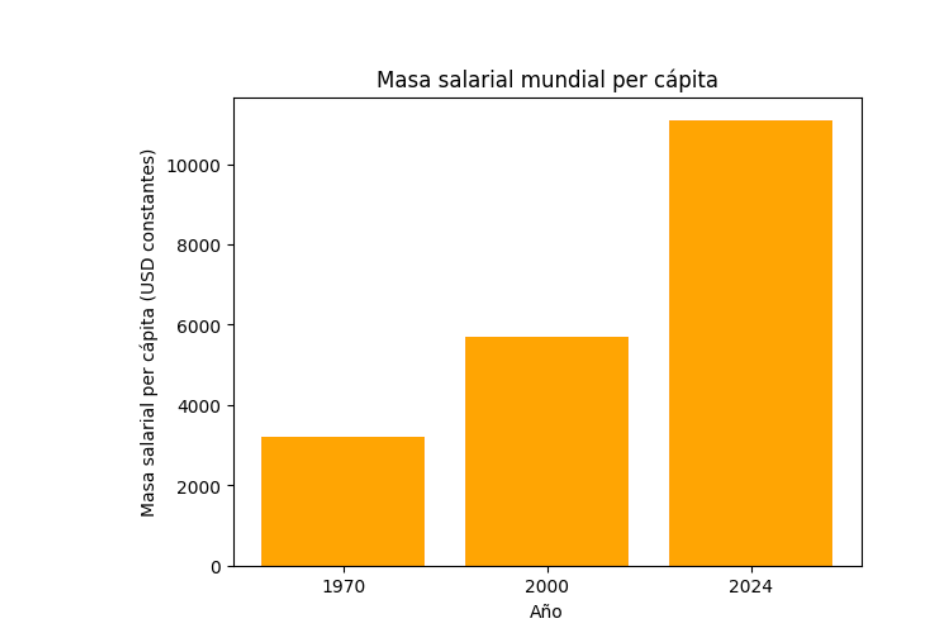
Si de porcentajes pasamos a cifras absolutas, resulta que en el año 2024, el gasto autonómico en España ascendió a los 254.000 millones de euros. Esto es, un gasto per cápita medio de 5.200 euros por habitante.

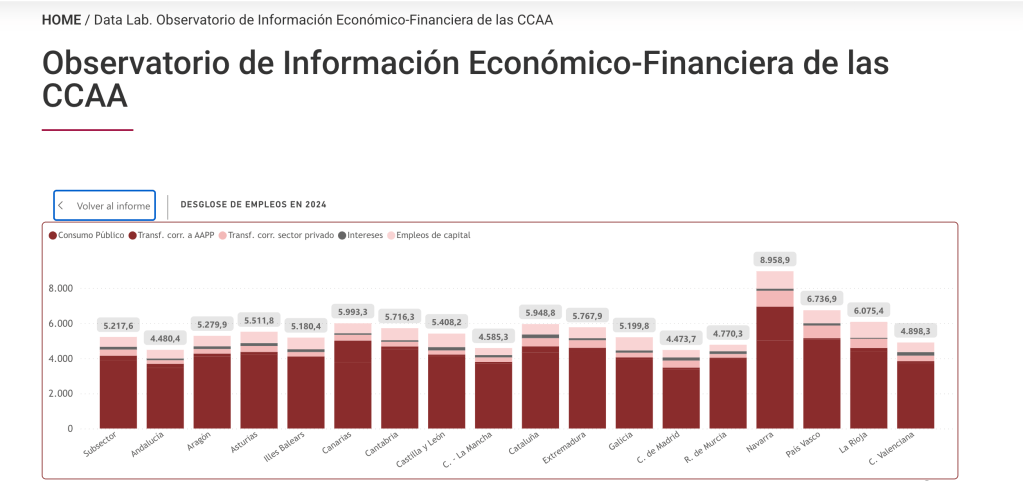
Pero, claro, esto es como lo de la tarta. Si somos dos y hay una tarta y me la como yo entera, según las estadísticas, cada uno de nosotros se habrá comido media tarta. ¿Cómo se traslada lo anterior a la distribución de gasto entre las distintas Comunidades Autónomas? Lo vemos en el siguiente gráfico, en el que están ordenadas las Comunidades Autónomas de mayor a menor gasto per cápita.

Los datos están extraídos de la Autoridad Independiente de Responsabilidad Fiscal:

2. ¿Explican las competencias autonómicas y la renta las diferencias de gasto?

Vemos que las diferencias entre unas y otras Comunidades Autónomas son muy notables. La que tiene un gasto mayor (Navarra) gasta ¡el doble! de la que tiene un gasto menor (Madrid). ¿Tiene esto sentido?

Para comentarlo, comenzaremos por dejar aclarado un tema recurrente: la diferencia de competencias entre unas Comunidades Autónomas y otras. Bien, algunas de esas competencias diferenciales no tienen un coste real. Por ejemplo, Galicia, País Vasco, Navarra, Aragón, Cataluña y Baleares tienen competencia en materia de Derecho Civil, mientras que el resto de Comunidades Autónomas no tienen esa competencia. Esa diferencia, en términos contables, ¿en qué se traduce? ¿En las dietas de los que forman parte de la Comisión de Codificación de la Comunidad Autónoma? Obviamente es un coste irrelevante.

Las competencias que sí tienen un impacto presupuestario son las de policía y prisiones, que tienen Cataluña, el País Vasco y Navarra (Navarra, solo policía, no prisiones); pero, ¿qué coste suponen? En el caso de Cataluña, los Mossos d’Esquadra tiene un coste de unos 250 euros anuales per cápita (un presupuesto de algo más de 2.000 millones de euros). La policía autonómica vasca es mucho más cara. Para una población que es poco más de una cuarta parte de la población catalana, el coste es de más de la mitad de los Mossos. El coste per cápita es casi tres veces mayor en el caso del País Vasco. En el conjunto de España, la cifra estará más cerca de los 250 euros de Cataluña que de los más de 600 en el País Vasco si se midiera el coste medio por habitante de un sistema policial único. En el caso de prisiones, el coste per cápita esta por debajo de los 50 euros.

Así pues, tanto en el País Vasco como en Navarra y en Cataluña podría asumirse un coste autonómico per cápita mayor respecto a la media teniendo en cuenta las competencias en materia de policía y prisiones, pero aún así la diferencia es, como se ha visto, mucho mayor.

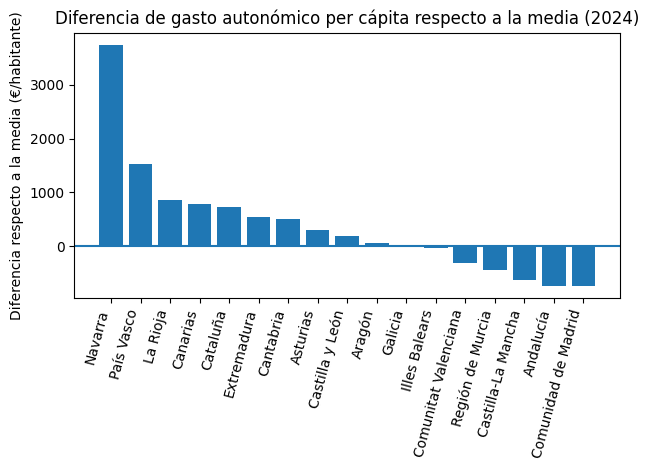
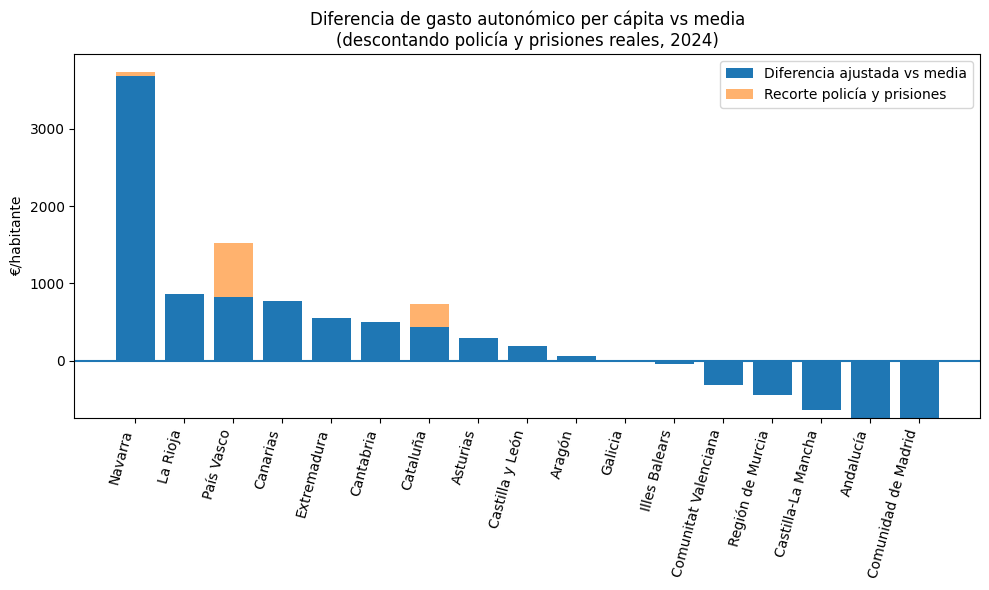
En el cuadro anterior se ve cómo queda la diferencia incluso descontando el gasto en cada Comunidad Autónoma en policía y prisiones. Sin entrar en ello, dejo apuntado que ese gasto es mayor del que resultaría de tener una policía para todo el Estado, lo que es especialmente claro en el caso del País Vasco. Esto es, si se toma la decisión de tener una policía autonómica, hay que ser consciente que supondrá un coste que habrá que sacar de algún otro lado (o pedir que te lo paguen otros). En el caso de España, la multiplicación de servicios autonómicos tiene, probablemente, un coste muy alto que, tan solo en el caso de la policía autonómica, puede cifrarse, sin ninguna exageración, en varios cientos de millones de euros.

Así pues, vemos cómo la diferencia de competencias entre unas y otras Comunidades Autónomas no explica las diferencias de gasto; incluso teniendo en cuenta las competencias ajustadas, hay Comunidades Autónomas con un gasto muy superior a la media y otras con un gasto muy inferior.

La renta per cápita tampoco explica estas diferencias, puesto que la Comunidad Autónoma con la mayor renta per cápita (Madrid) es también la que tiene un gasto per cápita autonómico menor. Obviamente, en el caso de Navarra y del País Vasco la explicación está en el régimen foral, que convierte a dichas Comunidades en espacios privilegiados; aunque, como han explicado con claridad Jesús Fernández-Villaverde y Francisco de la Torre (La factura del cupo catalán. Privilegios territoriales frente a ciudadanía, Madrid, La Esfera de los Libros, 2025, pp. 133-156, esp. pp. 154-155), gracias a que, pese a que la renta per cápita de esas regiones es superior a la media de España, son receptoras netos de solidaridad. La ausencia de economías de escala explica también, probablemente, la situación de La Rioja, la Comunidad Autónoma con menos población (poco más de 300.000 habitantes) y que, por tanto, ha de dividir entre un número muy pequeño los costes que supone toda administración autonómica. Canarias, por su parte, tiene una situación muy especial, tanto de insularidad (y una insularidad «archipelágica», porque junto a islas relativamente grandes hay otras más pequeñas que, sin embargo, han de disponer igualmente de servicios esenciales) como de lejanía respecto al resto de España, lo que, probablemente, explica también su mayor gasto autonómico per cápita.

Lo de que la renta per cápita explique tan poco es significativo, porque una parte relevante de los recursos autonómicos proceden de la participación en impuestos que vienen determinados por la capacidad económica de los contribuyentes; de tal manera que lo lógico es que dispongan de más recursos (y, por tanto, gasten más), aquellas Comunidades Autónomas con una renta per cápita superior. Si comparamos, en cambio, la renta per cápita de las Comunidades Autónomas con su gasto autonómico per cápita nos encontramos con algunas sorpresas:

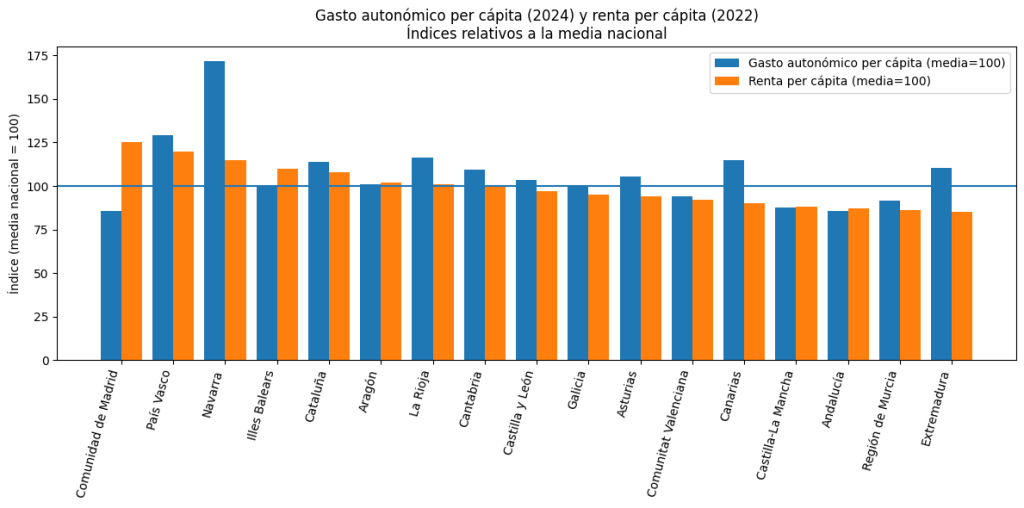
En este gráfico la renta per cápita es la del año 2022 (último dato disponible) mientras que el gaso es del año 2024.

Las Comunidades están ordenadas de mayor a menor renta per cápita y vemos cómo hay comunidades en las que el gasto per cápita prácticamente es igual a la renta per cápita (consideradas ambas magnitudes en relación a la media nacional). En este grupo estarían Aragón, Valencia, Castilla-La Mancha y Andalucía. Otro grupo lo forman aquellas Comunidades Autónomas que tienen un gasto autonómico proporcionalmente superior (o muy superior) a su renta per cápita (columna azul más alta que la columna naranja). En este grupo están el País Vasco, Navarra, Cataluña, La Rioja, Cantabria, Castilla y León, Galicia, Asturias, Canarias, Murcia y Extremadura) y, finalmente, un grupo en el que el gasto autonómico es inferior al que le correspondería por renta per cápita. Aquí están las Islas Baleares y, sobre todo, Madrid que, como hemos visto, es la primera Comunidad Autónoma por renta per cápita y la última por gasta autonómico per cápita.

Esto, ¿cómo puede ser? Pues no es fácil analizarlo, porque, como destacan en su libro Jesús Fernández-Villaverde y Francisco de la Torre, el sistema de financiación es confuso y, casi podíamos decir que deliberadamente confuso, probablemente por la utilización de una acumulación de criterios, discutibles cada uno de ellos, que, unidos, acaban convirtiendo en casi imposible elaborar análisis que resulten intuitivamente evidentes. Ahora bien, de lo que hemos visto hasta ahora se pueden extraer algunas conclusiones.

La primera, la más obvia, es que el sistema foral vasco y navarro chirría por decirlo suavemente. Las dos Comunidades Autónomas de régimen foral tienen un gasto per cápita que se sitúa claramente fuera del umbral en el que se mueven la mayoría de las demás comunidades.

La segunda. El pequeño tamaño de algunas Comunidades Autónomas, unido a la insularidad (Canarias) hace que el gasto per cápita aumente. Visto así se entiende que Navarra (medio millón de habitantes) muestre un gasto per cápita desorbitado, pues se une su condición foral con el pequeño tamaño de la Comunidad. La Rioja es otra Comunidad que tiene un gasto per cápita elevadísimo, lo que se corresponde con una Autonomía que tiene poco más de 300.000 habitantes.

La tercera. De las Comunidades Autónomas de régimen común con una renta per cápita superior a la media, la única con un gasto autonómico per cápita también superior a la media es Cataluña. Tanto Baleares como, sobre todo, Madrid, tienen un gasto per cápita inferior al que correspondería por su renta per cápita; lo que, seguramente, explica que otras Comunidades Autónomas puedan tener un gasto per cápita superior al que correspondería a su renta per cápita.

3. Dónde no está el dinero: sanidad y educación

Ahora bien, ¿a dónde va ese dinero de gasto autonómico en las Comunidades que gastan por encima de la media y, más concretamente, en aquellas Comunidades Autónomas que, teniendo una renta per cápita superior a la media también tienen un gasto autonómico per cápita superior a la media. Como veremos, no va a sanidad y educación.

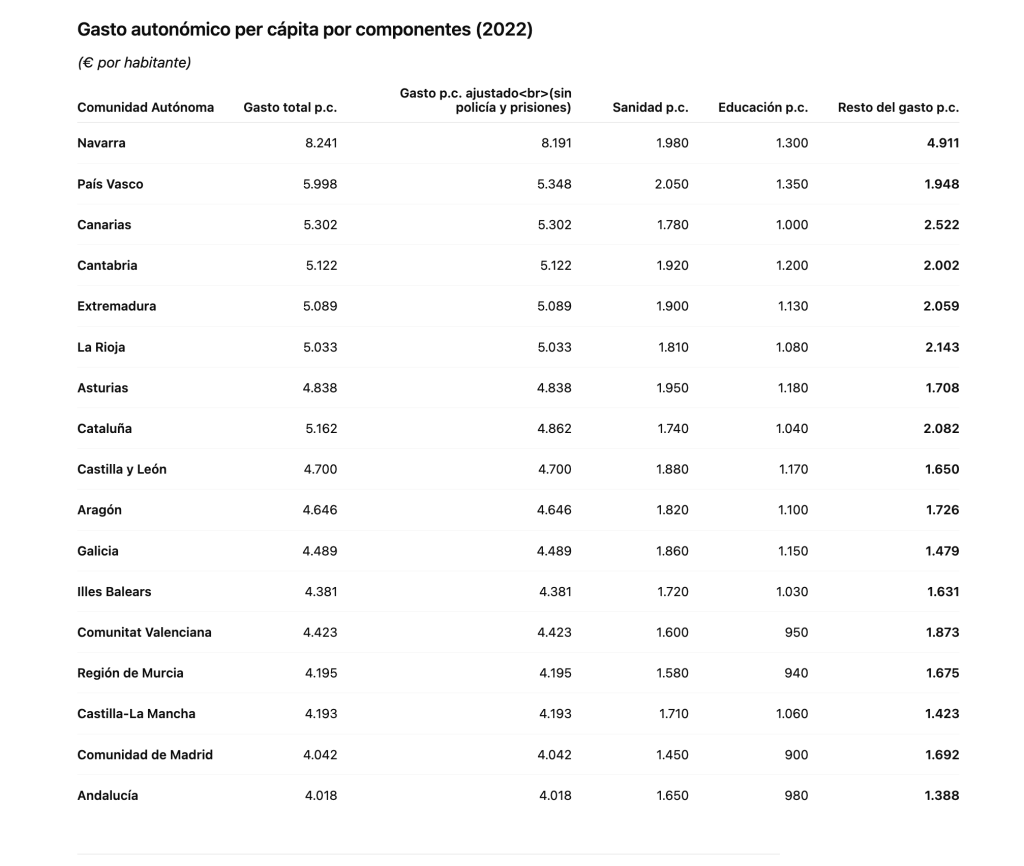
En esta tabla se ve el gasto per cápita del año 2022, el ajuste descontando policía y prisiones y la diferencia de gasto per cápita respecto a la media de toda España en sanidad y educación

Como puede apreciarse, el diferencial de gasto no se explica por educación o sanidad. En el caso de Navarra, el mayor gasto en esas partidas no explica siquiera una sexta parte de ese diferencial. En el del País Vasco, aún hay 123 euros per cápita que van más allá del gasto en sanidad y educación y en Cataluña los gastos de sanidad y educación no explican casi nada, pues están en la media nacional, de tal manera que su exceso de gasto ha de explicarse por otras vías (y, como ya hemos dicho, está excluido el gasto en las competencias específicas de policía y prisiones, que ya se han dejado fuera).

Es, por tanto, el resto del gasto autonómico (lo que no es sanidad y educación) lo que explica las diferencias entre Comunidades Autónomas.

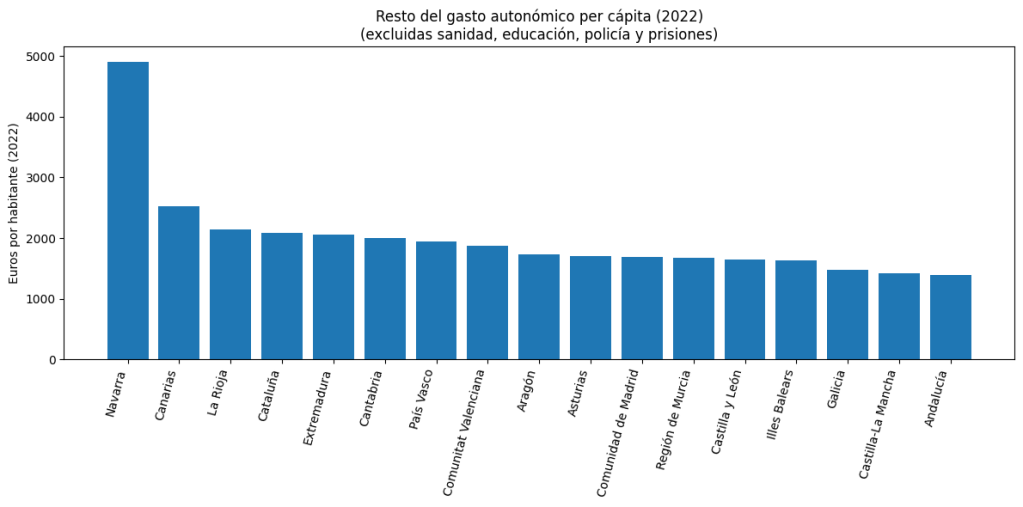
Como siempre, el pequeño tamaño de la Comunidad Autónoma tiene incidencia (Navarra, La Rioja, también Cantabria). La insularidad de Canarias está también presente; pero, aparte de esto, vemos que Cataluña se sitúa como una Comunidad donde el exceso de gasto que no va destinado a sanidad o educación tiene una incidencia relevante, más incluso que en el caso del País Vasco.

¿Por qué insisto en esto? Hay un mantra repetido según el cual las Comunidades Autónomas tienen que estar bien financiadas porque son las que atienden servicios tan esenciales como la sanidad y la educación; pero, como vemos, existen Comunidades Autónomas que tienen un gasto per cápita superior a la media de España y que, sin embargo, no tienen un gasto per cápita en sanidad y educación más alto que otras Comunidades Autónomas. En demasiadas ocasiones, la sanidad y la educación funcionan como coartadas discursivas para justificar incrementos de gasto autonómico que, en realidad, se desrtinan a otros fines. En algunos casos, políticas identitarias.

La evidente desigualdad entre Comunidades Autónomas, unido a la oscuridad del modelo de financiación autonómica también despierta (o debería despertar) suspicacias. ¿Cómo es posible que el gasto autonómico per cápita en Navarra sea el doble que en Madrid? Una de las razones es, obviamente, el régimen foral; otra, el mayor coste de las Comunides Autónomas más pequeñas. A esto se añade que hay determinadas estructuras (policías autonómicas) que resultan más caras al tener que renunciar a economías de escala. El caso de la policía autonómica vasca es, en este sentido, sangrante.

A lo anterior se añade que el constante mercadeo entre las fuerzas nacionalistas y el gobierno español conduce a un constante vaciamiento del Estado del que tenemos cumplida prueba con el reciente proyecto de modificación del sistema de financiación autonómica que se ha dado a conocer estos días. Tal y como veíamos al principio, las Comunidades Autónomas ya ahora suponen la parte principal del gasto público en España y se pretende que el «pastel» autonómico se aumente en 20.000 millones más que solamente podrán salir o de nuevos impuestos, de la creación de deuda pública, de las pensiones o de hacer todavía más pequeño el estado central. ¿Tiene sentido esto último cuando, como hemos visto, la falta de economía de escalas tiene un coste alto -quizás enorme- para el país?

¿Sería posible una reforma del sistema de financiación autonómica que introdujera cierta racionalidad? ¿Sería posible un sistema que, a partir de pocos parámetros, garantizara, a la vez, la igualdad en todos los servicios públicos esenciales y la suficiente autonomía a las Comunidades Autónomas? Finalmente, ¿sería posible tratar desde la racionalidad qué competencias tendrían que ser autonómicas y cuáles estatales o, por lo menos, que sepamos el coste -para todos- de competencias como las policías autonómicas?

4. Una propuesta simple para un sistema hoy disfuncional

Como hablar es gratis, propongo esta idea:

1) Se fija un suelo de gasto per cápita que se calcula mediante la suma del gasto per cápita en sanidad, educación y servicios sociales de las Comunidades Autónomas que ahora mismo más dedican a estas partidas. Ahora bien, no se trata de partidas finalistas, es solamente una manera para calcular ese suelo de la financiación autonómica. Ahora mismo este suelo quedaría establecido en 4.600 euros per cápita, teniendo en cuenta que en las tres partidas quien más gasta es el País Vasco (2050 euros per cápita en sanidad, 1350 euros en educación y unos 1200 euros en servicios sociales). Llamo la atención sobre que son cifras extraordinariamente altas en relación a otras Comunidades Autónomas; pero se trata de fijar un suelo que permita, con holgura, dar satisfacción a las necesidades sociales que tienen que atender las Comunidades Autónomas. No es un suelo austero, sino que se corresponde con el nivel de atención más alto que existe en España.

2) Se fija un techo en función de la renta per cápita de la Comunidad Autónoma respecto a la renta per cápita española. Es decir, una Comunidad Autónoma podría aumentar su gasto per cápita en relación al suelo en la misma proporción en la que su renta per cápita supera la renta per cápita española. Por supuesto, no sería obligado hacerlo, pero podría llegar hasta ese límite.

3) Si hubiera que atender situaciones especiales o particularidades (insularidad, por ejemplo) se haría con fondos estatales que no se transferirían a las Comunidades Autónomas, sino que serían gestionados por el Estado sin que supusieran compromisos permanentes y sin que se integraran en el sistema de financiación autonómica. El objetivo es que esas singularidades no se conviertan en derechos financieros permanentes.

4) Los recursos vendrían, como hasta ahora, básicamente de la cesión de parte de la recaudación de determinados impuestos con los ajustes necesarios para llegar a los niveles establecidos en los puntos 1 y 2.

Supone, obviamente, un cambio de modelo, porque sería el mismo para todas las Comunidades Autónomas, pero primaría la precaución, en tanto en cuanto no podría «esquilmarse» constantemente al Estado y, además, supondría asumir la responsabilidad de gestión de las competencias con los recursos de los que se dispone, y que no podrían incrementarse más que si aumenta la renta per cápita de la Comunidad Autónoma respecto a la media nacional. Por supuesto, el suelo, fijado inicialmente en 4.600 euros por habitante, también se iría ajustando en función del aumento de la renta per cápita en España.

¿Cómo quedaría el sistema de financiación autonómica con esta modificación? Se ve en el cuadro siguiente:

¿Duro? Recuerdo que el suelo se fija tomando las cantidades más altas con las que ahora se están prestando los servicios públicos de educación, sanidad y servicios sociales, y que el ajuste se hace a partir de la renta per cápita, porque un Estado complejo como España tiene que combinar la garantía de los servicios esenciales con la autonomía política de las Comunidades Autónomas; pero esa autonomía exige responsabilidad y no gastar por encima de las posibilidades que se tengan, porque la alternativa es que al final se devalúen las estructuras comunes a todo el país.

El ahorro que supondría este modelo se ve en el cuadro de abajo. Llamo la atención sobre Canarias que, obviamente, tiene que tener un trato especial como ya se ha indicado varias veces, por lo que parte al menos de los 3000 millones de ahorro tendrían que acabar revirtiendo por otras vías (punto 3 anterior). Ahora bien, llamo la atención que, incluso sin tener en cuenta la situación de Canarias, el ahorro que se conseguiría sería de unos 20.000 millones de euros, más de un 1% del PIB.

Pero más importante que el ahorro es el mensaje: se acabó el continuo deterioro del Estado a base de ir exigiendo cotas más altas de transferencias que, como hemos visto, no están justificadas por la atención a los servicios públicos esenciales.

Debemos repensar el modelo territorial español, pero hacerlo a partir de criterios racionales y de responsabilidad. Nos hemos descentralizado por encima de nuestras posiblidades y es hora de empezar a avanzar en la dirección contraria. Un estado complejo exige autonomía, pero también límies. Sin límites, la autonomía se convierte en irresponsabilidad, y sin responsabilidad fiscal, el Estado acaba siendo inviable.

Obviamente, la propuesta no pretende convertirse en realidad de un día para otro; pero creo que debería ser un objetivo que nos pusiéramos como país, porque la alternativa es el desastre a corto plazo, muy corto plazo, probablemente.

These are anxious times. Few people escape the unease born of a lingering suspicion: AI (artificial intelligence) will eventually destroy my job, and I will lose the means to earn a living. This is not an unfounded fear. For years now, the profession of translation has seen its work affected by machine-translation tools. In Spain, as I write this, a mass redundancy process (ERE) is being negotiated at a major company, Telefónica, where the firm argues that the use of AI allows it to dispense with thousands of jobs. But are we not, perhaps, facing one of those processes of creative destruction theorized by Schumpeter?

The magnitude of the change brought about by new technologies and AI may indeed give rise to doubt. Yet, even though the share of GDP devoted to labour compensation has been declining globally, economic growth has meant that the overall wage bill continues to increase, even in real terms.

This image shows the growth of the global wage bill in constant USD (equivalent to 2011 USD). The calculation is based on approximate global GDP figures and on the decline in labour’s share of that GDP. Whereas in 1970 this share stood at over 60%, by 2000 it had fallen to around 58%, and by 2024 it is below 55%. Nevertheless, real economic growth means that, despite this decline in labour’s share, the total amount of money reaching workers today is far higher than it was 25 years ago (almost three times as much) and vastly higher than it was 55 years ago (the current real wage bill—adjusted for inflation—is 7.5 times that of 1970).

In other words, “creative destruction” appears to be working. The disappearance of business models, professions, and economic structures is not accompanied by an impoverishment of workers. This can be seen not only in the growth of the global wage bill, but also in its per capita distribution. That is, if we divide the wage bill by the total population, the resulting figure also shows a steady increase.

Global wages per capita stood at around USD 3,200 in 1970, about USD 5,700 in 2000, and roughly USD 11,100 in 2024. As can be seen, this figure also increases, although at a slower pace than the global wage bill as a whole. While the global wage bill in 2024 was almost three times its level in 2000, wages per capita have “only” doubled. Likewise, whereas the 2024 wage bill was 7.5 times that of 1970, wages per capita in 2024 are less than four times their 1970 level.

One might ask why we calculate wages per capita by dividing by the total population rather than by the number of workers alone. There are two reasons. First, global population figures are relatively easy to obtain and involve little uncertainty, whereas there is far more ambiguity in estimating the total number of workers worldwide. The second reason, however, is more important. It has to do with the fact that wages are the most important mechanism for the distribution of wealth across the world. Virtually the entire global population depends, directly or indirectly, on labour income. This includes not only workers themselves, but also other members of their households. Dividing by the total population therefore gives us an approximate picture of how this mechanism of wealth redistribution actually operates.

In any case, and for our purposes, the technological innovations introduced over recent decades, together with the phenomenon of globalization, have not damaged either the overall wage bill or wages per capita. From an economic perspective, we should begin to worry only when wages per capita stop growing and, above all, when the global wage bill begins to decline. As long as this does not happen, the system is functioning: what is destroyed is offset by what is created. But is this enough?

The answer is no, because aggregate wage data do not yet tell us how wages are distributed among workers. If we look only at average wages without considering which wages are most common, statistics can be misleading. It may appear that everyone is doing better, when in fact it is the growth of high wages that drives up the average, while more modest wages may stagnate or even fall.

To examine this issue, we can use an index (which we will call R), defined as the ratio of the average wage (total wage bill divided by the number of full-time workers) to the median wage, that is, the wage that separates the top 50% of earners from the bottom 50%. The higher R is, the greater the concentration of wage growth at the top; the closer R is to 1, the more evenly wages are distributed across workers. This indicator does not measure poverty, but rather how wage growth is distributed.

To analyse R, we will not focus on the global level. Instead, we will look at four countries—United States, France, Germany, and Spain—and examine how this indicator has evolved from the year 2000 to the present.

As can be seen, R increases in all the countries considered; that is, wage inequality rises everywhere. This is most pronounced in the United States—where inequality was already higher than in European countries—but it is also evident in the other three cases. In Spain, wage inequality ultimately surpasses that of Germany and comes close to that of France.

The increase in wage inequality does not in any way undermine the creative nature of the destruction described by Schumpeter. For the economy as a whole, the changes brought about by technological improvements and global integration do not entail a loss in the value of labour: its remuneration continues to grow both in absolute terms and in relative (per capita) terms. What these changes do imply, however, is a different distribution of wages. Those who earn the most earn increasingly more, while lower-paid jobs gradually fall into a worse—at least relative—position. From a purely economic perspective, this need not be negative. Lower-quality jobs must eventually be abandoned so that labour can concentrate in activities that generate greater wealth. The fact that destruction is creative does not mean it ceases to be destruction and, therefore, it may involve personal costs; but these costs may be necessary so that, as we have seen, not only the economy as a whole, but also workers’ remuneration (for workers as a group) continues to increase. A different question is whether this inequality has social or political consequences—but these must be examined from a perspective other than a purely economic one. Before turning to that issue, however, one further factor must be taken into account.

Rising wage inequality implies that there are winners and losers; but the latter will be less disadvantaged in contexts of economic growth. If growth is sufficiently strong, inequality will not be perceived as a loss, because even if individuals lose relative position in the wage hierarchy, in absolute terms the perception will still be one of improvement. To incorporate this idea into the previous graph, one could introduce a correction factor based on each country’s growth rate. We will call the resulting index CI, defined by the following formula:

where c and t refer to the country and the year considered, and g to economic growth over the period in question (the preceding five years), adjusted by a parameter that allows us to assign greater or lesser weight to that growth. Using a correction factor of 0.5, the resulting values of CI for the countries considered are as follows:

Here we can see how economic growth alters the chart. As R (wage inequality) increases, the curve tends to move upwards; economic growth, by contrast, pushes it downwards. The outcome therefore differs from the previous chart because, for example, in the case of the United States, its strong growth means that although the R index (wage inequality) places it above all European countries (that is, in a worse position), once growth is taken into account it moves into a better position than they do. I developed this idea of linking inequality and growth in a post on this same blog a few months ago.

To go one step further, it is necessary to standardize the series by country. This is done using a tool known as the z-score, which replaces absolute index values with their deviation, in each case, from the historical mean of that economy. On this basis, the formula for the standardized CI index is as follows:

Where Z refers to the z-score of each variable. The resulting charts for each country, using this standardization, are as follows::

Standardization allows us to relate the evolution of the CI index to other indicators—specifically, the political polarization index available on the Our World in Data website (IPP). If we plot both standardized indices on the same chart, the country-specific results are as follows:

As can be seen, there is a clear correlation between the evolution of the CI index and political polarization. I noted earlier that, from a growth-centred economic perspective, the fact that “creative destruction” entails greater wage inequality is not necessarily a bad thing, since— as we have seen—both the overall wage bill and wages per capita continue to rise. In absolute and relative terms, therefore, “destruction” is beneficial for the labour market.

From a sociological or political perspective, however, the picture may be different. Inequality generates discontent which, when it is not offset by economic growth (hence the need to move from the R index to the CI index, which incorporates the growth factor), translates into political polarization: divisions deepen, opponents are stigmatized, and social tension increases. The previous charts show a correlation that cannot be ignored. As we can see, in all four countries considered, the CI index and the political polarization index follow a similar trajectory. In both Germany and France the correlation is almost perfect, except in 2010 (we will return to this shortly). In Spain the pattern is also similar, although polarization advances more rapidly than inequality, which may be attributed to factors that are not purely economic. Something similar occurs in the United States, where polarization has increased more rapidly than inequality in recent years—most likely reflecting the tensions surrounding the penultimate presidential election, including the storming of the Capitol.

It is also striking that in 2010 there is an increase in CI that is not accompanied by an equivalent rise in IPP. The most likely explanation for this divergence is that it coincides with the economic crisis of 2008–2010, a devastating shock that profoundly affected citizens. In Spain, measures were adopted that had previously been unthinkable (such as wage cuts for public-sector employees and the freezing of pensions), made possible by broad agreements among the major political forces (for example, the constitutional reform to guarantee debt repayment). This was a context in which discontent led to paralysis rather than confrontation. As is well known, in Spain and in other countries confrontation and polarization emerged somewhat later, whereas at the height of the crisis the immediate reaction was one of paralysis. This paralysis is reflected in the charts above, where we can see that in each country the rise of the blue line (CI) around 2010 is less pronounced than the movement of the orange line (IPP), with polarization even declining in France.

Based on what we have seen so far, it can be concluded that the technological changes of recent decades have not led to a decline in either the global wage bill or wages per capita. Creative destruction works.

What is happening, however, is a rise in wage inequality. Average wages increase because the remuneration of the highest-paid workers rises much faster than that of those at the bottom of the wage scale.

This inequality can be partially offset by economic growth; but even when growth is taken into account, we cannot ignore the correlation between rising inequality and increasing political polarization, which reflects growing tensions within society. Of course, inequality is not the only polarizing factor and, as we saw in 2010 (and as the charts confirm), in certain circumstances rising inequality can be more paralyzing than confrontational. Even so, it is difficult to dismiss the possibility that the growing polarization observed in the politics of many countries is, to some extent, related to rising wage inequalities, which appear to be a side effect of the “creative destruction” in which we have been immersed for decades.

This brings the post to a close. Its aim was to assess whether we are indeed witnessing a phase of creative destruction. The answer, in my view, must be affirmative as long as both the overall wage bill and wages per capita continue to grow. The inequalities that are being generated, however, may have consequences for society as a whole, as we have seen when considering the IPP. From this point on, the prescription is simple: if there is no growth, there must be equality; otherwise, social tensions may ultimately erupt—especially in contexts of declining institutional trust.

Son tiempos de temor. Pocos se libran de la angustia que nace de una sospecha: la IA (inteligencia artificial) acabará por destruir mi puesto de trabajo y perderé los medios para ganarme la vida. No es una sospecha infundada. Desde hace ya años, el gremio de los traductores ha visto su trabajo afectado por las herramientas de traducción automática. En España, cuando escribo esto, se está negociando un ERE en una gran compañía, Telefónica, en el que la empresa argumenta que con la utilización de la IA puede prescindir de miles de puestos de trabajo. Ahora bien, ¿no estaremos ante uno de esos procesos de destrucción creativa que teorizó Schumpeter?

La transcendencia del cambio que suponen las nuevas tecnologías y la IA puede hacer dudar. Sin embargo, pese a que la proporción del PIB que se destina a la remuneración del trabajo desciende de manera global, el crecimiento económico hace que la masa salarial aumente, incluso en términos reales.

En esta imagen se ve el crecimiento de la masa salarial mundial en USD constantes (equivalentes a USD del año 2011). El cálculo se hace teniendo en cuenta el PIB mundial aproximado y la disminución en la participación de los salarios en ese PIB. Mientras en 1970 se situaba por encima del 60%, en 2000 era de un 58% aproximadamente y en 2024 se sitúa por debajo del 55%. Ahora bien, el crecimiento real de la economía hace que, pese a esa disminución en la participación de los salarios, el total de dinero que llega a los trabajadores es mucho más ahora que hace 25 años (casi multipolica por 3 esa cifra) y muchísimo más que hace 55 años (la masa salarial actual multiplica en 7,5 la masa salarial real -descontando inflación- la de 1970).

Es decir, la «destrucción creativa» parece funcionar. La desaparición de modelos de negocio, profesiones y estructuras no va acompañada de un empobrecimiento de los trabajadores; lo que se aprecia ya no solo en la masa salarial global, sino también en su distribución per cápita. Esto es, si dividimos la masa salarial por el conjunto de la población también se aprecia un incremento constante de la cifra resultante.

La masa salarial per cápita en 1970 era de unos 3200 USD, en el año 2000 era de unos 5700 USD y en el año 2024, de unos 11100 USD. Como se ve, también aumenta; aunque en una proporción menor que la masa salarial global. La masa salarial global de 2024 multiplicaba casi por 3 la de 2000 y, en cambio, la masa salarial per cápita «solamente» la dobla. La masa salarial de 2024 era 7,5 veces la masa salarial de 1970, mientras que la masa salarial per cápita de 2024 es menos de 4 veces la de 1970.

La preguna aquí puede ser la de por qué calculamos la masa salarial per cápita dividiendo entre toda la población y no solamente entre los trabajadores. Las razones son dos. La primera, que la cifra de la población mundial es fácil de obtener y plantea pocas dudas, mientras que hay muchas más incertidumbres sobre cómo calcular la cifra global de trabajadores. La segunda razón, sin embargo, es más importante. Tiene que ver con que el salario es el mecanismo más importante para la distribución de la riqueza en el mundo. Prácticamente toda la población mundial vive de manera directa o indirecta del trabajo. Lo hacen los trabajadores, pero también otros miembros de su familia, de manera que la división entre el conjunto de la población nos da una idea aproximada de cómo funciona este mecanismo de redistribución de la riqueza.

En cualquier caso, y a nuestros fines, resulta que las innovaciones tecnológicas que se han introducido en las últimas décadas y el fenómeno de la globalización no han dañado ni el conjunto de la masa salarial ni la masa salarial per cápita. Deberíamos empezar a preocuparnos solo cuando la masa salarial per cápita no crezca y, sobre todo, si la masa salarial global disminuye. Si esto no sucede, desde una perspectiva económica, el sistema funciona: lo que se destruye se ve compensado por lo que se crea. Ahora bien, ¿nos basta con esto?

La respuesta es que no, porque los datos sobre el conjunto de la masa salarial no nos dicen todavía cómo se distribuye entre los trabajadores. Si tomamos los salarios medios sin considerar cuáles son los más frecuentes, la estadística nos puede tender una trampa; porque podría parecer que todo el mundo mejora cuando, en realidad, es el crecimiento de los salarios altos el que eleva el salario medio, mientras que los salarios más modestos pueden mantenerse o, incluso, descender.

Para examinar esta cuestión podemos utilizar un índice (que llamaremos R) que resulta de dividir el salario medio (dividir el conjunto de la masa salarial por el número de trabajadores a tiempo completo) por el salario mediano, esto es, el que separa al 50% de trabajadores que más ganan del 50% de los trabajadores que ganan menos. Cuando más alto sea R, mayor será la acumulación de salario en los salarios más altos; cuanto más cerca esté R de 1 más igualitaria será la distribución del salario entre todos los trabajadores. Este indicador no mide pobreza, sino cómo se reparte el crecimiento salarial.

Para examinar R no nos fijaremos en el nivel mundial, sino que consideraremos cuatro países: Estados Unidos, Francia, Alemania y España, y veremos cómo evoluciona ese indicador, R, entre el año 2000 y la actualidad.

Como puede apreciarse, en todos los países considerados R aumenta; esto es, la desigualdad salarial se incrementa. De manera más acusada en Estados Unidos (donde se partía ya de una desigualdad mayor que en los países europeos), pero también en los otros tres. En el caso de España, esa desigualdad acaba superando la de Alemania y acercándose a la de Francia.

El que aumente la desigualdad en la distribución de salarios en nada afecta al carácter creativo de la destrucción que explicó Schumpeter. Para el conjunto de la economía, los cambios derivados de las mejoras tecnológicas y de la integración mundial no suponen una pérdida de valor del trabajo, cuya remuneración sigue creciendo tanto en términos absolutos como relativos (per cápita); pero tales cambios sí que implican una distribución diferente de esos salarios. Quienes más ganan, cada vez ganan más; mientras que los trabajos peor remunerados van colocándose en una peor posición, al menos relativa. Esto en principio, desde una perspectiva económica, puede no ser negativo. Los empleos de peor calidad tienen que acabar siendo abandonados para que el trabajo se concentre en aquellas actividades que generan mayor riqueza; el hecho de que la destrucción sea creativa no quita que sea destrucción y, por tanto, puede tener costes personales; pero que resultarán necesarios para que, como hemos visto, no solamente el conjunto de la economía, sino también las retribuciones de los trabajadores (del conjunto de los trabajadores) aumente. Cuestión distinta es que esa desigualdad no tenga consecuencias sociales o políticas, pero estas deberán examinarse desde una perspectiva diferente a la puramente económica. Antes de pasar a ello, sin embargo, hay que tener en cuenta otro factor que examinaremos a continuación.

El aumento en la desigualdad de las retribuciones implica que hay ganadores y perdedores; pero estos últimos lo serán menos en contextos de crecimiento económico. Si el crecimiento es lo suficientemente importante, la desigualdad no se percibirá como pérdida, porque aunque se pierda posición relativa en la escala salarial, en términos absolutos la percepción será de mejora. Para integrar esta idea en la gráfica anterior podría establecerse un corrector basado en el índice de crecimiento de cada país. Llamaremos al índice resultate CI, siendo la fórmula del mismo la siguiente:

Donde c y t hacen referencia al país y año considerado y g al crecimiento en el período considerado (los cinco años precedentes), corregido por un indicador que nos permitirá dotar de más o menos peso a dicho crecimiento. Con un corrector de 0,5 el resultado del CI para los países considerados sería el siguiente:

Aquí se ve como el crecimiento económico modifica la gráfica. Al aumentar R (la desigualdad en los salarios) la gráfica tiende a ir hacia arriba; pero el crecimiento económico la llevaría hacia abajo. El resultado varía respecto al cuadro anterior porque, por ejemplo, en el caso de Estados Unidos, su alto crecimiento hace que mientras el índice R (desigualdad salarial) lo coloca por encima (esto es, en peor posición) que todos los países europeos; cuando se introduce el crecimiento pasa a estar en mejor situación que estos. Desarrollaba la idea de conectar desigualdad y crecimiento en una entrada de este mismo blog de hace unos meses.

Para ir un paso más allá es necesario estandarizar las series por país, lo que se hace mediante un instrumento denominado z-score que sustituye los valores absolutos del índice por la desviación, en cada caso, respecto a la media histórica en cada economía. De acuerdo con esto, la fórmula de CI ya estandarizado sería esta:

Donde Z hace referencia al z-score de cada magnitud. Las gráficas resultantes para cada país con esta estandarización serían las siguientes:

La estandarización nos permitirá relacionar la evolución del índice CI con otros índices; en concreto el índice de polarización política que se encuentra en la página web Our World in Data (IPP). Si colocamos en la misma gráfica los dos índices estandarizados, el resultado por país es como sigue:

Como puede apreciarse, existe una evidente correlación entre la evolución de CI y la de la polarización política. Antes indicaba que desde una perspectiva centrada en el crecimiento económico, el hecho de que la «destrucción creativa» implicara desigualdades en la distribución salarial no era necesariamente malo; puesto que, como veíamos, tanto la masa salarial como la masa salarial per cápita aumentaban. Esto es, en términos absolutos y relativos, para el mercado laboral la «destrucción» es provechosa.

Ahora bien, desde una perspectiva sociológica o política la perspectiva puede ser diferente. Las desigualdades crean malestar que, cuando no se ve compensado por el crecimiento económico (y de ahí la necesidad de pasar desde el índice R al índice CI, que tiene en cuenta el factor crecimiento) ese malestar se traduce en polarización política, se profundiza en la división, se estigmatiza al adversario y la crispación aumenta. Las gráficas anteriores muestran una correlación que no puede ser obviada. Como vemos, en los cuatro países considerados, la línea del índice CI y del índice de polarización política siguen un camino semejante. Tanto en Alemania como en Francia la correlación es casi perfecta excepto en 2010 (ahora iremos a eso). En España la línea también es parecida, aunque la polarización avanza más rápido que la desigualdad; lo que puede achacarse a factores que no son puramente económicos. En Estados Unidos sucede algo parecido, la polarización aumenta más rápido que la desigualdad en los últimos años; lo que, seguramente, tiene que ver con la tensión vivida durante la penúltima elección presidencial, asalto al Capitolio incluido.

Llama la atención también que en 2010 se aprecia un aumento de CI que no va acompañado de un aumento equivalente de IPP. Probablemente la explicación de esa divergencia se encuentre en que se corresponde con la crisis económica de los años 2008-2010, una crisis devastadora que provocó un tremendo shock en los ciudadanos. En España se adoptaron medidas que nunca habían sido imaginadas (reducción de salarios de los empleados públicos y congelación de las pensiones, por ejemplo), lo que fue posible por los grandes acuerdos a los que llegaron las fuerzas mayoritarias (reforma de la Constitución para garantizar el pago de la deuda, por ejemplo). Es un contexto en el que el malestar paraliza en lugar de confrontar. Como es sabido, en España y en otros países la confrontación y polarización apareció un poco después, mientras que en el mismo momento de la crisis la reacción fue de parálasis. Una parálisis que se aprecia en los gráficos anteriores, donde se ve cómo en cada país, la subida de la línea azul (CI) en torno a 2010 es menos pronunciado que el ascenso de la línea naranja (IPP), llegándose, incluso, al descenso de tal polarización en Francia.

De acuerdo con lo que se ha visto hasta ahora, se constata que los cambios tecnológicos de los últimos lustros no han supuesto ni una disminución de la masa salarial mundial ni una disminución de la masa salarial per cápita. La destrucción creativa funciona.

Lo que sí se está produciendo es el aumento de la desigualdad en los salarios. El salario medio se incrementa porque suben en mayor medida las remuneraciones de los trabajadores mejor pagados que la de aquellos que se encuentran en la parte baja de la tabla salarial.

Esta desigualdad se puede ver compensada en parte por el crecimiento económico; pero ni siquiera teniendo este en cuenta podemos obviar que existe una correlación entre aumento de la desigualdad e incremento de la polarización política, lo que es una muestra del incremento de las tensiones dentro de la sociedad. Por supuesto, no es el único factor polarizador y, además, como vimos en 2010 (y se corrobora en los gráficos), en ciertas ocasiones el aumento de la desigualdad puede ser más paralizante que otra cosa. Aún así, no creo que pueda dejarse de lado la posibilidad de considerar que la creciente polarización que se observa en la política de muchos países alguna relación tiene con el aumento en las desigualdades salariales que parece ser un efecto secundario de la «destrucción creativa» en la que llevamos décadas inmersos.

Hasta aquí esta entrada, que tenía por objeto verificar si realmente estamos asistiendo a una fase de destrucción creativa. La respuesta creo que ha de ser afirmativa en tanto en cuanto la masa salarial y la masa salarial per cápita crezcan. Ahora bien, las desigualdades que se están generando pueden tener consecuencias en el conjunto de la sociedad, como hemos visto al considerar el IPP. A partir de aquí la receta es sencilla: si no hay crecimiento, ha de haber igualdad; de otra forma, la tensión en la sociedad puede acabar estallando, especialmente en contextos de desconfianza institucional.

Physics knows the constant c, the speed of light in a vacuum. Anyone who has approached this science cannot help but be fascinated by that value, which seems to contain within it the entire complexity of the Universe. Despite its simple formulation (299,792.458 kilometers per second), its implications for almost everything— from time dilation to gravity or the expansion of the Universe—make it difficult to grasp fully.

Economics, too, has a mysterious constant: the rate of return on capital (r). Economics is not physics, of course; and for r we cannot give an eternally immutable figure as we can for c. Yet it should surprise us that, over centuries, r has remained on average between 4% and 5%. Whether we look at eighteenth-century London, nineteenth-century Paris, or twentieth-century New York, we find that the average return on capital oscillates around those same percentages. It is not (on average—individual cases may vary widely) 1%, nor is it 15%; it is almost always between 4% and 5% (Th. Piketty, Capital in the Twenty-First Century, The Belknap Press of Harvard University, 2014, Kindle edition, location 8%).

Why is the rate of return on capital so constant? I do not think we have a clear explanation, but I will risk putting forward a hypothesis.

To introduce it, I suggest we step back to the time of the Roman Empire and focus on something that seems quite distant from our modern economy: the slave markets. How much was a slave worth in Rome? According to the sources available, in the first and second centuries CE, in Egypt, an ordinary slave might cost between 300 and 500 denarii—that is, between 90 and 150 grams of gold. To this purchase price one had to add food, lodging, and very little else. All of that might amount to roughly 100 denarii per year (about 30 grams of gold).

Thus, if one purchased a 15-year-old slave who remained productive for another 15 years (the life expectancy of slaves engaged in demanding labor rarely exceeded their early thirties, and beyond that age their performance likely declined), the total cost of that slave over a 15-year period would amount to between 1,800 and 2,000 denarii (roughly 540 to 600 grams of gold).

What return did the owner obtain from such a slave? The daily earnings of an unskilled free laborer were approximately 1 denarius. A slave working 270 days per year would therefore generate 4,050 denarii over 15 years. Those 270 days imply an almost continuous workload, with few days of rest (around 60 per year). In other words, an investment of 1,800–2,000 denarii would yield a profit of between 2,000 and 2,200 denarii over 15 years. That is, about 130 to 145 denarii per year—corresponding to an annual return of roughly 6.5% to 8%.

This is not the 4–5% typical of the modern era, but it does coincide with what appear to have been the returns on capital in the Roman Empire (between 6% and 8%, with 12% being the legal maximum). Interestingly, that 6.5–8% range aligns with the simple result of dividing the investment by the slave’s useful working life. If we assume that r ≈ 1/L, where L is the slave’s working life, then with L = 15 years we obtain r ≈ 6.7%, and with L = 12.5 years, r ≈ 8%. Life expectancy at birth in Rome was around 20–25 years, but anyone who reached adolescence could expect to live another 15–20 years, although the wear of manual labor meant that performance would decline after the age of 30. A working-life range of 12 to 15 years is therefore plausible.

In any case, these are averages; for an 18-year-old slave (perhaps the ideal age, since one might expect full adult productivity throughout those years), the purchase price would be higher, which would naturally adjust r back toward the relationship noted above (r ≈ 1/L). There is no need to go further here: the point is simply that it is not unreasonable to think that the return on capital embodied in a slave (purchase price plus maintenance costs) could be understood as a function of that capital and the slave’s useful working life.

It is as if the economic structure incorporated a temporal horizon determined by the duration of working life. From that horizon r would emerge. Put differently: the economy discounts human life.

If we now return to the familiar 4–5% with which we began, we can see that expressing it in relation to working life—not of the slave but of the modern worker—introduces a certain coherence. A 4% return corresponds to a working life of roughly 25 years; 5% to about 20 years. For the eighteenth or nineteenth centuries, these figures are not implausible. After the age of 40–45, many manual workers experienced a decline in effectiveness, not to mention illness, injury, or premature death. It is therefore not unreasonable to think that this seemingly constant rate of return might be linked to the length of people’s productive working lives.

Similarly, the slow decrease in returns observed over recent decades may be connected to the extension of fully productive working life—a working life that now begins later, closer to 25 than to 20, due to longer periods of education, and that extends beyond 50, whereas in an era dominated by manual labor that age already marked the end of full productivity. The point is not to be exact, but simply to underline that the useful life of the worker determines the order of magnitude of the rate of return.

Thus, as a provisional hypothesis (if the redundancy may be forgiven), we may suggest that the rate of return on capital is determined by the average useful length of working life. This would explain the higher returns observed in antiquity (when working lives were shorter) and the slow decline in the rate of return over the past century, linked to the gradual extension of working life—a working life that, as noted above, now begins later for most people than it did a hundred years ago (due to longer periods of education) but also extends beyond 50, an age that in an era of predominantly manual labor marked the end of full productive capacity.

There is, moreover, another striking constant in what we have been observing. If we return to the Roman slave who costs between 300 and 500 denarii, works for 15 years, and generates for his owner the equivalent of 270 denarii per year, we find that of those 270 denarii the owner’s profit is slightly more than half. Recall that maintaining the slave might cost around 100 denarii per year, to which one must add the amortization of the purchase price. If the slave cost 300 denarii, that amortization is 20 denarii per year; if he cost 500, it is somewhat over 30. Taking a midpoint, the owner’s profit from the slave comes to 145 denarii—about 53%.

It is striking that this share of income—which we might say goes to capital—is of the same order of magnitude as what we observe today. According to standard national accounts, the share of capital in total income currently stands at around 45% of GDP, after having risen from the levels of the 1960s, when it was below 40%. A change of more than 13% (from the 53% we observed in the Roman example, to around 40% in the 1960s) is undoubtedly significant; but we are speaking of twenty centuries, and nothing dictates that this share must be close to 50% rather than 10% or 90%. By the same token, one must ask why the rate of return on capital remains around 5% both two thousand years ago and today.

It is true that there are enormous differences between slave labor and wage labor; yet one cannot ignore the structural elements that place them in relation. Under slavery, subordination to the master is total; under wage labor, that subordination is only partial and temporary, but it nonetheless involves submitting to the employer’s direction during working time—albeit in exchange for a wage that has no equivalent in slavery. Needless to say, the point here is not to equate slavery and wage labor from a moral standpoint, but to remain faithful to the underlying economic reality that both phenomena share.

Now, as we have seen, acquiring a slave involves a maintenance cost (food, shelter, clothing) to which the purchase price must be added (setting aside cases in which the slave is born into slavery). If we add together the cost of maintaining the slave and the amortization of the purchase price over the slave’s useful working life, the resulting amount is of the same order of magnitude as a modern wage—except that under slavery the purchase price is paid to a third party, whereas under wage labor it accrues to the worker. In a certain sense, this “purchase price” is incorporated into the wage.

There is therefore no essential difference between the Roman model and the modern one. Both the distribution between capital and labor and the rate of return on capital fall within similar ranges, provided we take into account that in the modern case the equivalent of the slave’s acquisition cost is embedded in the wage.

It is tempting, then, to project this Roman example onto the present. The basis for doing so is the idea that r ≈ 1/L. The average useful working life of the worker determines the rate of return obtained on capital. In a way, that return reflects how the hourglass of working life (and of physical life as well) empties grain by grain; and it is for this reason that as working life lengthens, r declines, even if only slightly. The same total amount of benefit must be spread over a longer period, and the annual return is therefore lower.

The cost of the slave (purchase price plus maintenance over the entire useful working life—that is, C + M*L, where C is the purchase price, M the annual maintenance cost, and L the duration of working life) constitutes the capital that makes the generation of profit possible. In the modern world, the equivalent would be the capital (K) required for the functioning of the economy. Here we must take into account that if r ≈ 1/L and Sc is the share of income that accrues to capital, then the amount of capital needed to sustain that relationship cannot be measured by summing up existing assets; it must instead be understood through the temporal scale defined by L. Capital (K) is not measured—it is inferred.

Accordingly, the calculation of K follows from considering the share of capital in GDP (GDP minus labor costs, which we denote Sc), divided by r (that is, by 1/L); in other words, Sc*L. The capital required to generate the observed return is thus the capital share of income multiplied by the length of working life.

The result is far greater than what one obtains by summing a country’s assets in the manner used by Piketty in his studies of capital, because in this framework capital includes the cost of raising, educating, and training workers, as well as all other conditions that make economic functioning possible. With a capital share of 40% of GDP, the resulting K—for an r of 4.5%—would amount to 12.5 times GDP. In the Roman example, the resulting K would be 7.5 times annual output (2,025 denarii for an annual output of 270). This means that in Rome capital represented a smaller proportion of income than today, but still one far larger than what emerges from attempts to “count” existing assets in a given economy.

I am fully aware that this is not the usual way of calculating the capital stock of an economy; yet it is the only way to account for everything that is actually required for production. The Roman slave example, in its simplicity, contains all the necessary elements. Here, the workforce is “capitalized” in an evident way through the right of ownership. The fact that, today, the relationship between worker and employer differs fundamentally—in legal, moral, and political terms—from that of a slave society should not obscure the structural point: in both cases, the relationship between capital and labour is organised in essentially the same way, as we have already suggested.

What changes is that part of the cost of “maintaining” the worker is now externalized—borne either by society as a whole (basic public services) or by the family that has raised and educated the worker. Excluding these elements from the measurement of capital explains the difference between the result of this approach (K = Sc*L) and that obtained by trying to quantify existing assets at a given moment. The two approaches do not measure the same thing: one measures the structural capacity to sustain labour; the other measures the ownership of assets.

In the end, this is only a hypothesis—an attempt to link that persistent mystery (the remarkable constancy of the return on capital) with something tangible: the duration of human life, or more specifically, the span of our working life. The return on capital is nothing more than the shadow that our lives cast upon the economy.

La física conoce la constante «c», la velocidad de la luz en el vacío. Nadie que se haya acercado a esta ciencia dejará de estar fascinado por ese valor que parece encerrar toda la complejidad del Universo. Pese a que su formulación es sencilla (299.792,458 kilómetros por segundo), las implicaciones que tiene en casi todo; desde la contracción del tiempo hasta la gravedad o la expansión del Universo la hacen difícil de aprehender. En economía hay también una constante misteriosa: la rentabilidad del capital (r). La economía no es física; y para r no podemos dar una cantidad eternamente inmutable como para c; pero debería sorprendernos que durante siglos, de media, se ha mantenido entre un 4% y un 5%. Tanto si estamos en el Londres del siglo XVIII o en el París del XIX o en el Nueva York del XX observaremos como el rendimiento medio del capital oscila en esos porcentajes. No es (de media, insisto, para casos particulares puede haber valores muy diferentes) ni un 1% ni un 15%; casi siempre entre el 4% y el 5% (Th. Piketty, «Capital in the Twenty-First Century», The Belknap Press of Harvard University, 2014, 8% de la edición Kindle).

¿Por qué esa tasa constante de rendimiento del capital? Me parece que no hay una explicación para ello; pero me arriesgo a lanzar una hipótesis.

Para formular la hipótesis propongo retroceder hasta la época del Imperio Romano y detenernos en algo que parece bastante alejado de nuestra economía moderna: los mercados de esclavos. ¿Cuánto valía un esclavo en Roma? Según las fuentes disponibles, en el siglo I-II d.C, en Egipto, un esclavo ordinario podía valer entre 300 y 500 denarios; esto es, entre 90 y 150 gramos de oro. A este coste habría que añadir la alimentación, alojamiento y, seguramente, muy poca cosa más. Todas estas cosas podían implicar unos 100 denarios al año (unos 30 gramos de oro).

Así pues, si se adquiría un esclavo de 15 años y rendía durante otros 15 años (la esperanza de vida de los esclavos en Roma para los trabajos exigentes no superaba en mucho los 30 años y, a partir de esa edad, probablemente su rendimiento sería menor), tenemos que el coste de un esclavo durante un periodo de 15 sería de entre 1800 y 2000 denarios (entre 540 y 600 gramos de oro).

¿Qué rendimiento obtenía el amo por ese esclavo? Los ingresos diarios de un trabajador libre no cualificado eran de aproximadamente 1 denario. Un esclavo que trabajara 270 días al año daría un rendimiento en 15 años de 4050 denarios. Los 270 días implican un trabajo casi constante, con pocos descansos (unos 60 días al año). O, lo que es lo mismo, una inversión de 1800-2000 denarios produce un beneficio de entre 2000 y 2200 denarios en 15 años. Esto es, entre 130 y 145 denarios anuales; lo que implica un rendimiento que se sitúa entre el 6,5% y el 8% anual.

No es el 4%-5% de la Edad Moderna, sino algo superior; pero que coincide con lo que parece ser que eran los rendimientos del capital en el Imperio Romano (el interés para los préstamos se situaba entre el 6% y el 8%, siendo el 12% anual el máximo legal permitido). Curiosamente, ese 6,5%-8% se correlaciona con el resultado de dividir la inversión por los años de vida útil del esclavo. Si asumimos que r ≈ 1/L, siendo L la vida útil del esclavo, si L es 15 años r ​se sitúa en un 6,7%; mientras que con una vida útil de 12,5 años, r sería de un 8%. La esperanza de vida al nacer en Roma se situaba entre los 20-25 años; pero quien ya había llegado a la adolescencia podía esperar vivir entre 15 y 20 años más; aunque el desgaste del trabajo haría que el rendimiento fuera menor a partir de los 30 años, como se ha adelantado. Esto es, un rango de vida útil de entre 12 y 15 años es plausible. De cualquier forma, aquí estamos hablando de medias; esto es, en el caso de un esclavo de 18 años (quizás la edad ideal, pues se puede esperar que trabaje durante toda su vida adulta), el precio sería mayor, por lo que r se ajustaría de manera natural a la relación que veíamos antes (r ≈ 1/L). Aquí no hace falta ir más allá porque tan solo se trata de apuntar que no es descabellado pensar que el rendimiento del capital que suponía un esclavo (precio de adquisición más costes de mantenimiento) podría establecerse como una relación entre ese capital y la vida útil del esclavo como trabajador. Pareciera que la estructura económica incorpora un horizonte temporal que viene determinado por la duración de la vida laboral. De ese horizonte se derivaría r. Dicho de otra forma: la economía descuenta la vida humana.

Si ahora volvemos al famoso 4%-5% con el que comenzábamos; vemos que si lo expresamos también en relación con la vida productiva, ya no del esclavo, sino del trabajador, algo de coherencia podría aparecer. Un 4% se correspondería a 25 años de vida laboral; 5% a 20 años. Si pensamos en los siglos XVIII o XIX no parecen cifras carentes de sentido. A partir de los 40-45 años, en muchos trabajos manuales el trabajador pierde eficacia, sin contar con enfermedades, lesiones o muertes prematuras; esto es, durante esos siglos, quizás no es desabellado pensar que esa rentabilidad mágicamente constante se relaciona con el tiempo de actividad productiva de las personas. De igual forma, el lento decrecimiento de las rentabilidades en las últimas décadas podría también relacionarse con la extensión de la vida laboral plenamente productiva; una vida laboral que ahora comienza más tarde, más cerca de los 25 años que de los 20, y que se extiende a más allá de los 50. Aquí no se trata de ser exactos, sino tan solo de subrayar que la vida útil del trabajador determina el orden de magnitud de la rentabilidad.

Así pues, como hipótesis provisional (perdón por la redundancia), podemos avanzar que la rentabilidad del capital se determina por la extensión útil media de la vida laboral. Eso explicaría unas mayores rentabilidades en la edad Antigua (vida laboral más corta) y la lenta disminución de los rendimientos del capital en el último siglo, vinculado a una cierta extensión de la vida laboral; una vida laboral que, como se ha adelantado, comienza más tarde para la mayoría que hace un siglo (extensión de los estudios superiores), pero que también se prolonga más allá de los 50 años que, en época de trabajo fundamentalmente manual marcaban el fin de la vida plenamente útil del trabajador.

Existe, además, otra constante llamativa en lo que vamos viendo. Si volvemos al esclavo romano que cuesta entre 300 y 500 denarios, trabaja 15 años y obtiene para su amo el equivalente a 270 denarios, resulta que de esos 270 denarios el beneficio para el dueño es de algo más de la mitad. Recordemos que el mantenimiento del esclavo podía suponer unos 100 denarios al año, a lo que habíaque sumar la amortización del precio de compra. Con 300 denarios, esa amortización es de 20 denarios al año; con 500, de algo más de 30. Si nos colocamos en el rango intermedio, el beneficio que obtiene el amo del esclavo es de 145 denarios, un 53%.

Sorprende que esta parte de la renta que -podríamos decir- va al capital, es del mismo orden que la que encontramos en la actualidad. La participación del capital en la renta se sitúa en la actualidad, de acuerdo con las contabilidades habituales, en torno al 45% del PIB, apreciándose un aumento desde los años 60 del siglo XX, en el que esa participación era de menos de un 40%. Ciertamente, una variación de más de un 13% (del 53% que veíamos en el mundo romano a partir de nuestro modesto «experimento», al 40% en los años 60 del siglo XX) es más que significativa; pero estamos hablando de veinte siglos y en ningún sitio está escrito que esa participación tuviera que ser del orden del 50% y no del 10% o del 90%; de igual forma que habría que ver por qué el rendimiento del capital se mueve en torno al 5% tanto hace dos mil años como ahora.

Es verdad que hay enormes diferencias entre el trabajo de los esclavos y el trabajo asalariado; pero no puede desconocerse que existen elementos estructurales que los ponen en relación. En la esclavitud el sometimiento al amo es total; mientras que el trabajo asalariado, ese sometimiento es solamente parcial y temporal, pero también se asemejan en que se asume ponerse bajo la dirección del empresario durante el tiempo de trabajo; aunque aquí a cambio de un salario que no existe en el caso de la esclavitud. Obvio es decirlo, aquí no se está equiparando esclavitud y trabajo desde una perspectiva moral, sino que se intenta ser fiel a la realidad económica que subyace en ambos fenómenos.

Ahora bien, como vemos, la adquisición de un esclavo tiene un coste de mantenimiento (alimentación, cobijo, vestido) al que hay que sumar el precio que se pagó por el esclavo (aparte de los casos en los que se trate de hijos de esclavas que ya nacen también esclavos). Si se suma el coste de mantenimiento del esclavo y la amortización de su precio de adquisición durante su vida útil, la cantidad resultante se coloca en el mismo orden que el salario actual, con la diferencia de que en la esclavitud el precio de compra va a un tercero mientras que, en el trabajo asalariado, revierte en el trabajador. De alguna forma, ese «precio de compra» se incorpora al salario.

No hay, por tanto, una diferencia esencial entre el modelo romano y el actual. Tanto la distribución entre capital y trabajo como la rentabilidad del capital se mueven en unos parámetros similares si tenemos en cuenta que ahora en el trabajo tenemos que incorporar lo que sería el coste de adquisición del esclavo en el mundo romano.

Resulta tentador proyectar este ejemplo del mundo romano sobre el actual. La base para ello es la idea de que r ≈ 1/L. La vida útil media del trabajador determina el rendimiento que se obtiene por el capital. De alguna forma, el rendimiento muestra cómo el reloj de la vida laboral (y también de la física) se va vaciando de arena; es por eso que a medida que la vida laboral se alarga, r disminuye aunque sea ligeramente. Al final la cantidad de beneficio ha de distribuirse en más tiempo y, por tanto, el rendimiento anual disminuye.

El coste del esclavo (precio de compra más mantenimiento durante toda su vida útil; esto es, C+ML, donde C es el precio de compra, M el coste anual de mantenimiento y L la duración de su vida laboral) es el capital que permite la generación del beneficio. En la actualidad, el equivalente sería el capital (K) necesario para el funcionamiento de la economía. Aquí tenemos que tener en cuenta que si r ≈ 1/L y Pc es la parte de la renta que va al capital; entonces la cantidad de capital necesaria para sostener esa relación no puede medirse por la suma de activos; sino por la escala temporal que marca L. El capital no se mide, se deduce. De acuerdo con esto, el cálculo de K se derivaría de considerar la participación del capital en el PIB (PIB menos costes salariales, a lo que denominaremos Pc), divido por r (1/L); esto es, Pc*L. Es decir, el capital necesario para generar el rendimiento observado es la renta del capital multiplicado por los años de vida laboral. El resultado es mucho mayor que lo que resulta de sumar los activos de un país en la vía que empleó Piketty en sus estudios sobre el capital, pero porque aquí el capital incluye el coste de crianza, educación y formación de los trabajadores; así como el resto de condiciones que hacen posible el funcionamiento de la economía. Con una participación del capital del 40% del PIB, el K resultante sería, para una r de 4,5%, 12,5 veces el PIB. Piénsese que en el ejemplo del esclavo romano, la K resultante sería de 7,5 veces la renta anual (2025 denarios para una renta anual de 270 denarios). Esto es el capital en Roma representaba una proporción menor que ahora respecto a la renta; pero en magnitudes superiores a las que se consideran mediante el método de intentar contar los activos existentes en una determinada economía.

Soy consciente de que esta no es la forma habitual de calcular el capital para una economía determinada; pero es de esta forma como puede tenerse en cuenta todo aquello que es necesario para la producción. El ejemplo del esclavo romano, en su sencillez, encierra todos los elementos precisos. Aquí la fuerza de trabajo está «capitalizada» de una manera evidente a través del derecho de propiedad. El hecho de que, en la actualidad, las relaciones del trabajador con el empresario se alejen esencialmente (en lo legal, moral y político) de lo propio en una sociedad esclavista no puede hacernos perder de vista que desde una perspectiva estructural, las relaciones entre capital y trabajo se articulan de una forma esencialmente idéntica, tal y como adelantamos. Lo que sucede es que una parte del coste necesario para el «mantenimiento» del trabajador se externaliza, pues lo asume o el conjunto de la sociedad (servicios públicos esenciales) o la familia que lo ha criado y educado. El dejar fuera de la contabilización del capital estos aspectos explica la diferencia entre lo que resulta de esta aproximación (K=Pc*L) de la que parte de intentar cuantificar los activos existentes en un momento dado. Ambas aproximaciones no miden lo mismo: una mide la capacidad estructural para sostener el trabajo, la otra, la propiedad de los activos.

En fin, se trata solo de una hipótesis. Un intento de vincular ese misterio (la constancia en la rentabilidad del capital) con una realidad tangible: la duración de la vida humana o, más específicamente, el tiempo de nuestra vida laboral. El rendimiento del capital no es más que la sombra que proyecta nuestra vida sobre la economía.